Optimized Multi-Location P-rep Design
Source:vignettes/multi_location_prep.Rmd
multi_location_prep.RmdThis vignette shows how to generate an optimized
multi-location partially replicated (p-rep) design using both
the FielDHub Shiny App and the scripting function
multi_location_prep() from the FielDHub R
package.
Overview
Partially replicated (p-rep) designs are commonly employed in early generation field trials. This type of design is characterized by replication of a portion of the entries, with the remaining entries only appearing once in the experiment. Commonly, the part of treatments with reps is due to an arbitrary decision by the research, also in some cases, it is due to technical reasons. The replication ratio is typically 1:4 (Cullis 2006), which means that the portion of treatment repeated twice is p = 25%. However, the design can be adapted to meet specific needs by adjusting the values of and the level of replication. For example, standard varieties (checks) may be included with higher levels of replication than test lines.
In FielDHub, the optimized multi-location p-rep design
employs the principles of incomplete block designs (IBD) to determine
the distribution of replicated and non-replicated treatments across
multiple locations.
Optimization
Across Location
The function multi_location_prep() uses the incomplete
blocks design approach (Edmondson 2020) to
optimize the allocation of replicated and un-replicated treatments
across the environments.
Within Location
Each partially replicated (p-rep) design location undergoes an optimization process that involves the following procedure:
Given a matrix of integers (p-rep design within location), we want to ensure that the distance between any two occurrences of the same treatment is at least a distance . More specifically, we want to modify to ensure that no treatments appear twice within a distance less than in the resulting matrix.
The goal of the optimization process is to find a modified matrix
that satisfies this constraint while maximizing some measure of
deviation from the original matrix
.
In this case, the measure of deviation is the pairwise Euclidean
distance between occurrences of the same treatment. The process is done
by the function swap_pairs() that uses a heuristic
algorithm that starts with a distance of
between pairs of occurrences of the same treatment, and increases this
distance by
and repeats the process until either the algorithm no longer converges
or the maximum number of iterations is reached.
The algorithm works by first identifying all pairs of occurrences of the same treatment that are closer than . For each such pair, the function selects a random occurrence of a different integer that is at least away, and swaps the two occurrences. This process is repeated until no further swaps can be made that increase the pairwise Euclidean distances between occurrences of the same treatment.
Toy Example
Consider a p-rep design where ten treatments are replicated twice and 40 only once. The matrix (field layout) for this experiment has 6 rows and 10 columns.
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
[1,] 21 40 17 25 26 3 11 31 36 6
[2,] 5 5 33 8 48 29 43 23 1 45
[3,] 41 27 38 39 7 28 14 22 24 4
[4,] 4 47 18 7 2 35 6 20 12 46
[5,] 3 15 9 34 49 50 2 10 42 8
[6,] 32 16 19 9 10 13 37 1 44 30In this initial p-rep design, we notice that the two instances of treatment 5 are positioned next to each other. Additionally, treatments 7 and 9 are also situated in adjacent cells. These suboptimal allocations could lead to issues or inaccurate results when analyzing the data from this experiment due to the short distance between replicated treatments and the likely spatial correlation between them.
The following table shows the pairwise distances for the replicated treatments
geno Pos1 Pos2 DIST rA cA rB cB
5 5 2 8 1.000000 2 1 2 2
7 7 22 27 1.414214 4 4 3 5
9 9 17 24 1.414214 5 3 6 4
2 2 28 41 2.236068 4 5 5 7
10 10 30 47 3.162278 6 5 5 8
1 1 48 50 4.123106 6 8 2 9
6 6 40 55 4.242641 4 7 1 10
3 3 5 31 6.403124 5 1 1 6
8 8 20 59 6.708204 2 4 5 10
4 4 4 57 9.055385 4 1 3 10Swap pairs
We can improve the efficiency of the design by swapping the
treatments that are close and next to each other by using the function
swap_pairs() from FielDHub R package.
library(FielDHub)
B <- swap_pairs(X, starting_dist = 3)The new matrix or the optimized p-rep design is,
print(B$optim_design)
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
[1,] 8 35 6 2 33 44 3 4 37 6
[2,] 43 30 25 5 39 29 19 11 36 45
[3,] 40 13 38 10 20 28 15 41 10 17
[4,] 1 27 18 31 32 22 24 21 12 5
[5,] 23 47 3 34 49 50 16 46 14 48
[6,] 7 26 2 42 9 1 8 7 4 9The distances for each pairwise of treatments are,
print(B$pairwise_distance)
geno Pos1 Pos2 DIST rA cA rB cB
9 9 30 60 5.000000 6 5 6 10
10 10 21 51 5.000000 3 4 3 9
2 2 18 19 5.099020 6 3 1 4
4 4 43 54 5.099020 1 8 6 9
1 1 4 36 5.385165 4 1 6 6
3 3 17 37 5.656854 5 3 1 7
5 5 20 58 6.324555 2 4 4 10
6 6 13 55 7.000000 1 3 1 10
7 7 6 48 7.000000 6 1 6 8
8 8 1 42 7.810250 1 1 6 7As we can see, the minimum distance that the algorithm reached is 5. This means no treatments appear twice within a distance less than 5 in the resulting prep design. It is a considerable improvement from the first version of the p-rep design
The FielDHub function multi_location_prep()
does internally all the optimization process and uses the function
swap_pairs() to maximize the distance between replicated
treatments.
Use case (Multi-Location P-rep Design)
Suppose there is a plant breeding field trial with 150 entries to be tested across five environments, where up to seven replications of each entry are allowed. Additionally, the project includes three checks; each replicated six times. We can generate an optimized multi-location partially replicated design using these parameters. This strategy guarantees that all treatments are present in all environments but in different amounts of replications.
We can generate this design using the FielDHub Shiny app and the
FielDHub multi_location_prep() standalone
function in R.
1. Using the FielDHub Shiny App
Once the app is running, click the tab Partially Replicated Design and select Optimized Multi-Location p-rep from the dropdown.
Then, follow the following steps where we will show how to generate an optimized partially replicated design.
Inputs
-
Import entries’ list? Choose whether to import a list with entry numbers and names for genotypes or treatments.
If the selection is
No, that means the app is going to generate synthetic data for entries and names of the treatment/genotypes based on the user inputs.If the selection is
Yes, the entries list must fulfill a specific format and must be a.csvfile. The file must have the columnsENTRYandNAME. TheENTRYcolumn must have a unique entry integer number for each treatment/genotype. The columnNAMEmust have a unique name that identifies each treatment/genotype. BothENTRYandNAMEmust be unique, duplicates are not allowed. In the following table, we show an example of the entries list format.
| ENTRY | NAME |
|---|---|
| 1 | Genotype1 |
| 2 | Genotype2 |
| 3 | Genotype3 |
| 4 | Genotype4 |
| 5 | Genotype5 |
| 6 | Genotype6 |
| 7 | Genotype7 |
| 8 | Genotype8 |
| 9 | Genotype9 |
| 10 | Genotype10 |
Enter the number of entries in the Input # of Entries box as a comma separated list. In our example we will have 150 entries, so we enter 150 in the box for our sample experiment.
Select whether or not the experiment will contain checks under the Include checks? option. The example experiment does, so set this to
Yes.Once we select
Yeson the above option, two more boxes appear, the first being Input # of Checks where we set how many checks to include in the experiment. In our case this is 3.Next to this option we have Input # Check’s Reps, where we set the number of replications for each check respectively in a comma separated list. We are replicating each of the 3 checks 6 times, so enter
6,6,6in this box.Enter the number of locations in Input # of Locations. We will run this experiment over 5 locations, so set Input # of Locations to 5.
Set the total number of replications of the entries over all locations in the
# of Copies Per Entrydropdown box. For this example experiment, set this to 7.Select
serpentineorcartesianin the Plot Order Layout. For this example we will use the defaultserpentinelayout.To ensure that randomizations are consistent across sessions, we can set a random seed in the box labeled Random Seed. In this example, we will set it to
2456.(Optional) Enter the starting plot number in the Starting Plot Number box. Since the experiment has multiple locations, you must enter a comma separated list of numbers the length of the number of locations for the input to be valid. In this example, we will set it as
1,1001,2001,3001,4001.(Optional) Enter the location names in the Input Location Name box. Since the experiment has six locations, you must enter a comma separated list of strings for the names of the environments. In this example, we will set it as
LOC1,LOC2,LOC3,LOC4,LOC5.
Once we have entered the information for our experiment on the left
side panel, click the Run! button to run the design.
You will then be prompted to select the dimensions of the field from the
list of options in the dropdown in the middle of the screen with the box
labeled Select dimensions of field. In our case, we
will select 12 x 19. Click the Randomize!
button to randomize the experiment with the set field dimensions and to
see the output plots. If you change the dimensions again, you must
re-randomize.
If you change any of the inputs on the left side panel after running an experiment initially, you have to click the Run and Randomize buttons again, to re-run with the new inputs.
Outputs
After you run a Optimized Multi-Location P-rep Design in
FielDHub and set the dimensions of the field, there are several ways to
display the information contained in the field book. The first tab,
Get Random, shows the option to change the dimensions
of the field and re-randomize, as well as the genotype allocation matrix
generated for the optimized p-rep design, which displays the
replications of each genotype over each location, much like the matrix
generated in sparse allocation.
Randomized Field
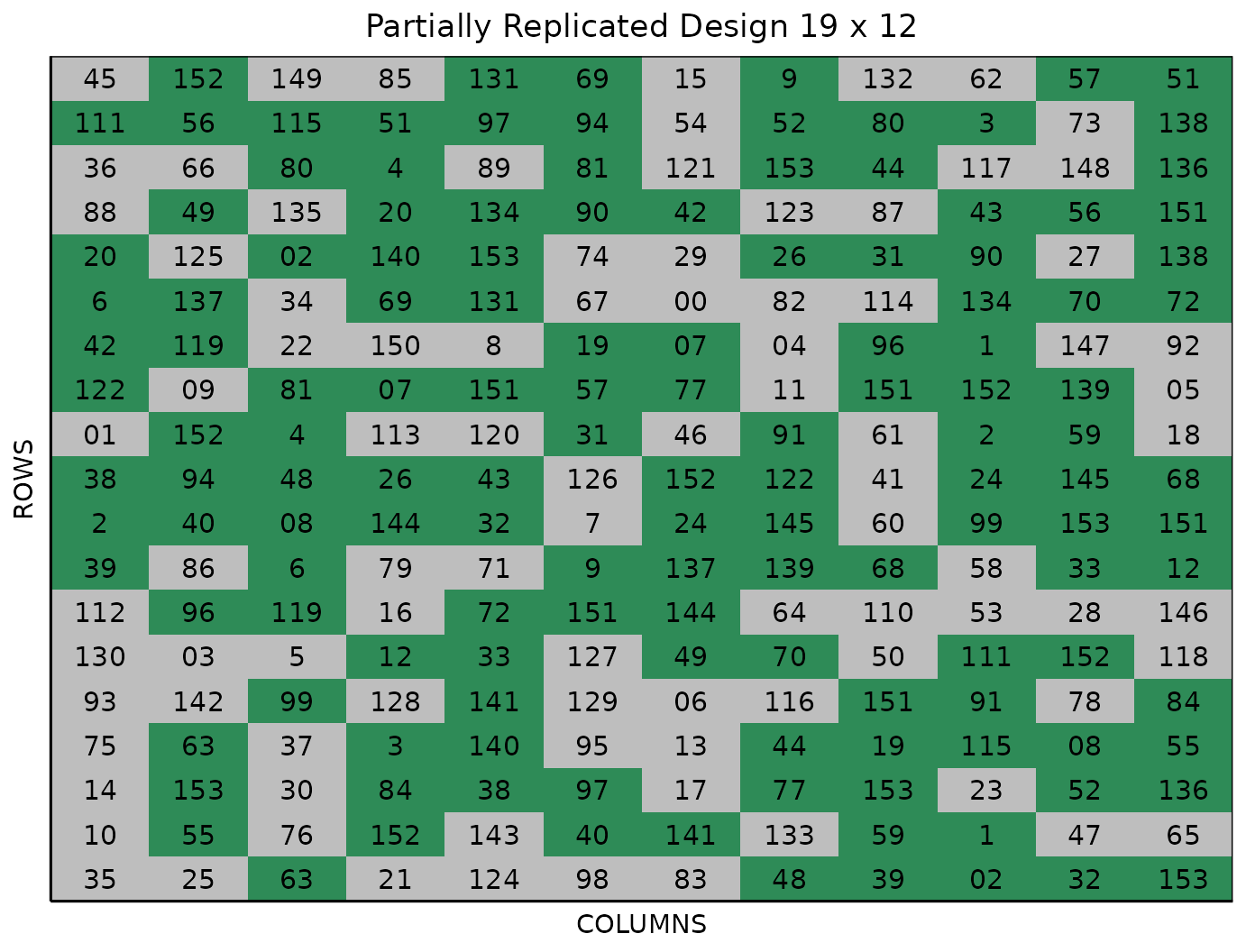
The Randomized Field tab displays a graphical representation of the randomization of the entries in a field of the specified dimensions. The replicated entries are the green colored cells, with the which cells appearing only once in the location. The display includes numbered labels for the rows and columns. You can copy the field as a table or save it directly as an Excel file with the Copy and Excel buttons at the top.
Plot Number Field
On the Plot Number Field tab, there is a table display of the field with the plots numbered according to the Plot Order Layout specified, either serpentine or cartesian. You can see the corresponding entries for each plot number in the field book. Like the Randomized Field tab, you can copy the table or save it as an Excel file with the Copy and Excel buttons.
Field Book
The Field Book displays all the information on the experimental design in a table format. It contains the specific plot number and the row and column address of each entry, as well as the corresponding treatment/genotype on that plot. This table is searchable, and we can filter the data in relevant columns.
2. Using the FielDHub function:
multi_location_prep().
You can run the same design with the function
multi_location_prep() in the FielDHub
package.
First, you need to load the FielDHub package typing,
Then, you can enter the information describing the above design like this:
optim_multi_prep <- multi_location_prep(
lines = 150,
l = 5,
copies_per_entry = 7,
checks = 3,
rep_checks = c(6,6,6),
plotNumber = c(1,1001,2001,3001,4001),
locationNames = c("LOC1", "LOC2", "LOC3", "LOC4", "LOC5"),
seed = 2456
)Details on the inputs entered in multi_location_prep()
above
The description for the inputs that we used to generate the design,
-
lines = 150is the number of entries in the field. -
l = 5is the number of locations. -
copies_per_entry = 7is the number of copies of each entry. -
checks = 3is the (optional) number of checks. -
rep_checks = c(6,6,6)is the (optional) number of replications of each check, in a vector the length of the number of checks. -
locationNames = c("LOC1", "LOC2", "LOC3", "LOC4", "LOC5")are optional names for the locations. -
seed = 2456is the random seed to replicate identical randomizations.
Print optim_multi_prep object
To print a summary of the information that is in the object
optim_multi_prep, we can use the generic function
print().
The multi_location_prep() function returns all the same
objects as in partially_replicated() and in addition
list_locs, allocation, and
size_locations. The object list_locs is a list
of data frames. Each data frame has three columns; ENTRY,
NAME and REPS with the information to
randomize to each environment. The object allocation is the
binary allocation matrix of genotypes to locations, and
size_locations is a data frame with a column for each
location and a row indicating the size of the location (number of field
plots).
For example, we can display the allocation object. Let
us print the first ten genotypes allocation.
LOC1 LOC2 LOC3 LOC4 LOC5
1 2 1 1 1 2
2 1 2 1 1 2
3 2 1 1 1 2
4 1 1 2 1 2
5 1 1 2 2 1
6 1 2 1 1 2
7 2 1 2 1 1
8 1 2 2 1 1
9 1 1 2 1 2
10 2 2 1 1 1Let us add two new columns to the allocation table. We can add the number of copies by genotype; it should be 7 for all of them. We can also add the average allocation by genotype. Each treatment will appear 1.4 times in average.
| LOC1 | LOC2 | LOC3 | LOC4 | LOC5 | Copies | Avg | |
|---|---|---|---|---|---|---|---|
| Gen-1 | 2 | 1 | 1 | 1 | 2 | 7 | 1.4 |
| Gen-2 | 1 | 2 | 1 | 1 | 2 | 7 | 1.4 |
| Gen-3 | 2 | 1 | 1 | 1 | 2 | 7 | 1.4 |
| Gen-4 | 1 | 1 | 2 | 1 | 2 | 7 | 1.4 |
| Gen-5 | 1 | 1 | 2 | 2 | 1 | 7 | 1.4 |
| Gen-6 | 1 | 2 | 1 | 1 | 2 | 7 | 1.4 |
| Gen-7 | 2 | 1 | 2 | 1 | 1 | 7 | 1.4 |
| Gen-8 | 1 | 2 | 2 | 1 | 1 | 7 | 1.4 |
| Gen-9 | 1 | 1 | 2 | 1 | 2 | 7 | 1.4 |
| Gen-10 | 2 | 2 | 1 | 1 | 1 | 7 | 1.4 |
We can manipulate the optim_multi_prep object as any
other list in R. We can first display the design parameters for the
randomizations with the following code:
print(optim_multi_prep)which outputs:
Multi-Location Partially Replicated Design
Replications within location:
LOCATION Replicated Unreplicated
1 LOC1 63 90
2 LOC2 63 90
3 LOC3 63 90
4 LOC4 63 90
5 LOC5 63 90
Information on the design parameters:
List of 7
$ rows : num [1:5] 19 19 19 19 19
$ columns : num [1:5] 12 12 12 12 12
$ min_distance : num [1:5] 3 3 3 3 3
$ incidence_in_rows: num [1:5] 4 2 3 5 2
$ locations : num 5
$ planter : chr "serpentine"
$ seed : num 2456
10 First observations of the data frame with the partially_replicated field book:
ID EXPT LOCATION YEAR PLOT ROW COLUMN CHECKS ENTRY TREATMENT
1 1 PrepExpt LOC1 2024 1 1 1 76 76 G-76
2 2 PrepExpt LOC1 2024 2 1 2 0 111 G-111
3 3 PrepExpt LOC1 2024 3 1 3 129 129 G-129
4 4 PrepExpt LOC1 2024 4 1 4 45 45 G-45
5 5 PrepExpt LOC1 2024 5 1 5 0 133 G-133
6 6 PrepExpt LOC1 2024 6 1 6 0 49 G-49
7 7 PrepExpt LOC1 2024 7 1 7 123 123 G-123
8 8 PrepExpt LOC1 2024 8 1 8 0 57 G-57
9 9 PrepExpt LOC1 2024 9 1 9 54 54 G-54
10 10 PrepExpt LOC1 2024 10 1 10 125 125 G-125Access to optim_multi_prep output
All objects are accessible by the $ operator,
i.e. optim_multi_prep$layoutRandom[[1]] for
LOC1, optim_multi_prep$fieldBook for the
fieldBook with all locations.
optim_multi_prep$fieldBook is a data frame containing
information about every plot in the field, with information about the
location of the plot and the treatment in each plot. As seen in the
output below, the field book has columns for ID,
EXPT, LOCATION, YEAR,
PLOT, ROW, COLUMN,
CHECKS, ENTRY, and TREATMENT.
Let us see the first 10 rows of the field book for this experiment.
field_book <- optim_multi_prep$fieldBook
head(field_book, 10) ID EXPT LOCATION YEAR PLOT ROW COLUMN CHECKS ENTRY TREATMENT
1 1 PrepExpt LOC1 2024 1 1 1 76 76 G-76
2 2 PrepExpt LOC1 2024 2 1 2 0 111 G-111
3 3 PrepExpt LOC1 2024 3 1 3 129 129 G-129
4 4 PrepExpt LOC1 2024 4 1 4 45 45 G-45
5 5 PrepExpt LOC1 2024 5 1 5 0 133 G-133
6 6 PrepExpt LOC1 2024 6 1 6 0 49 G-49
7 7 PrepExpt LOC1 2024 7 1 7 123 123 G-123
8 8 PrepExpt LOC1 2024 8 1 8 0 57 G-57
9 9 PrepExpt LOC1 2024 9 1 9 54 54 G-54
10 10 PrepExpt LOC1 2024 10 1 10 125 125 G-125Plot field layout
For plotting the layout in function of the coordinates
ROW and COLUMN in the field book object we can
use the generic function plot() as follows. This plots only
the first location, but this is indexable by location using the dollar
sign operator as well.
Field Layout for Location 1
plot(optim_multi_prep, l = 1)
In the figure above, green plots contain replicated entries, and gray plots contain entries that only appear once.
